用动态规划求解字符串常见问题

Mar 27, 2016

最长递归子序列

题目

给定数组arr,返回arr中的最长递增子序列，如arr=[2,1,5,3,6,4,8,9,7],返回的最长递增子序列为[1,3,4,8,9]

题解思路

先用DP来求解子序列递增的最大长度，如arr的长度序列为dp=[1,1,2,2,3,3,4,5,4]，然后对这个长度序列dp从右到左遍历，得到最长递增子序列。

  1. 求解长度序列，令dp[i]表示在以arr[i]这个数结尾的情况下，arr[0…i]中的最大递增子序列的长度。
    则状态转移方程为:dp[i]=max{dp[j]+1(0<=j<i,arr[j]<arr[i])}

  2. 然后遍历dp数组，从右向左,如dp=[1,1,2,2,3,3,4,5,4]，先找到最大值为5，索引为7，即’9’，前一个数则应该是4，索引为6，即’8’；重复该步骤即可；

该方法时间复杂度为O(N^2)

如果在求解dp数组的过程中采用二分查找来进行优化，可以将复杂度降低到O(N*logN)

class LIS
    {
    public:
        LIS(vector<int> _nums) :nums(_nums){}
        //获得最长递增子序列
        vector<int> get_lis()
        {
            vector<int> len_dp = get_length();
            vector<int> ret = solve_lis(len_dp);
            return ret;
        }
    private:
        vector<int> nums;
        //dp求解长度
        vector<int> get_length()
        {
            //状态转移方程为：dp[i]=max{dp[j]+1(0<=j<i,arr[j]<arr[i])}
            vector<int> ret(nums.size(), 1);
            for (int i = 0; i < nums.size(); i++)
            {
                for (int j = 0; j < i; j++)
                {
                    if (nums[j] < nums[i])
                        ret[i] = max(ret[i], ret[j] + 1);
                }
            }
            return ret;
        }
        //从右向左获取最长递增子序列
        vector<int> solve_lis(vector<int> len_dp)
        {
            int len = 0;
            int index = 0;
            //先找到最大长度和索引
            for (int i = 0; i < len_dp.size(); i++)
            {
                if (len_dp[i] > len)
                {
                    len = len_dp[i];
                    index = i;
                }
            }
            //从右向左遍历
            vector<int> ret(len, 0);
            ret[--len] = nums[index];
            for (int i = index; i >= 0; i--)
            {
                if (nums[i] < nums[index] && len_dp[i] == len_dp[index] - 1)
                {
                    ret[--len] = nums[i];
                    index = i;
                }
            }
            return ret;
        }
    };

最长公共子串

题目

给定两个字符串str1和str2，返回两个字符串的最长公共字串，如str1=’1AB2345CD’,str2=’12345EF’,返回’2345’

解题思路

经典的动态规划方法的时间复杂度为O(M*N)，空间复杂度为O(M*N)，采用压缩优化后，可将空间复杂度优化至O(1) dp[i][j]表示将str1[i]和str2[j]作为公共字串的最后一个字符，公共字串的长度。则：
状态转移方程为：dp[i+1,j+1]=(str1[i]==str2[j])?dp[i,j]+1:0;

//最长公共字串，经典DP问题
string longestCommonSubstring(const string& str1, const string& str2)
{
    size_t size1 = str1.size();
    size_t size2 = str2.size();
    if (size1 == 0 || size2 == 0) return 0;

    vector<vector<int> > dp(size1, vector<int>(size2, 0));

    // 初始化
    for (int i = 0; i < size1; ++i)
    {
        dp[i][0] = (str1[i] == str2[0] ? 1 : 0);
    }
    for (int j = 0; j < size2; ++j)
    {
        dp[0][j] = (str1[0] == str2[j] ? 1 : 0);
    }
    //dp
    for (int i = 1; i < size1; ++i)
    {
        for (int j = 1; j < size2; ++j)
        {
            if (str1[i] == str2[j])
            {
                dp[i][j] = dp[i - 1][j - 1] + 1;
            }
        }
    }
    //找字串,max为长度，end_ix表示字串结束位置
    int max = 0;
    int end_idx = 0;
    for (int i = 0; i < size1; ++i)
    {
        for (int j = 0; j < size2; ++j)
        {
            if (max < dp[i][j])
            {
                max = dp[i][j];
                end_idx = i;
            }
        }
    }
    //获取字串并返回
    return str1.substr(end_idx - max + 1, max);
}

优化思路：因为计算每个dp[i][j]时只用到了其左上方的dp[i-1][j-1]，所以只需要一个变量即可，即空间复杂度为O(1)
Alt text

最长公共子序列

题目

给定两个字符串str1和str2，返回两个字符串的最长公共子序列

思路

状态转移方式：
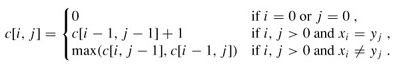
Alt text
c[i][j]记录str1[i]与str2[j] 的LCS 的长度

  
//最长公共子序列,时间辅助度和空间辅助度都是O(M*N)
string get_lcs_subsequece(string str1, string str2)
{
    vector<vector<int>> dp(str1.size(), vector<int>(str2.size(), 0));
    dp[0][0] = str1[0] == str2[0] ? 1 : 0;
    for (int i = 1; i < str1.length(); i++)
    {
        dp[i][0] = max(dp[i - 1][0], str1[i] == str2[0] ? 1 : 0);
    }
    for (int j = 1; j < str2.length(); j++)
    {
        dp[0][j] = max(dp[0][j - 1], str1[0] == str2[j] ? 1 : 0);
    }
    for (int i = 1; i < str1.length(); i++)
    {
        for (int j = 1; j < str2.length(); j++)
        {
            dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]);
            if (str1[i] == str2[j])
            {
                dp[i][j] = max(dp[i][j], dp[i - 1][j - 1] + 1);
            }
        }
    }
    //获取子序列
    int m = str1.size()-1;
    int n = str2.size()-1;
    string res;
    int index = dp[m][n]-1;
    while (index >= 0)
    {
        if (n > 0 && dp[m][n] == dp[m][n - 1])
        {
            n--;
        }
        else if (m > 0 && dp[m][n] == dp[m - 1][n])
        {
            m--;
        }
        else
        {
            res.insert(res.begin(), str1[m]);
            index--;
            /*res[index--] = str1[m];*/
            m--;
            n--;
        }
    }
    return res;
}

编辑距离

题目

传送leetcode Edit Distance

解题思路：

设状态为 f[i][j]，表示 A[0,i] 和 B[0,j] 之间的最小编辑距离。设 A[0,i] 的形式是 str1c，B[0,j] 的形式是 str2d，

  1. 如果 c==d，则 f[i][j]=f[i-1][j-1]；
  2. 如果 c!=d，
  • 如果将 c 替换成 d，则 f[i][j]=f[i-1][j-1]+1；
  • 如果在 c 后面添加一个 d，则 f[i][j]=f[i][j-1]+1；
  • 如果将 c 删除，则 f[i][j]=f[i-1][j]+1；
  
// LeetCode, Edit Distance
// 二维动规，时间复杂度 O(n*m)，空间复杂度 O(n*m)/*Edit Distance*/
int minDistance(string word1, string word2)
{
    if (word1 == "" && word2=="") return 0;
    vector<vector<int>> dis(word1.size()+1, vector<int>(word2.size()+1, 0));
    for (size_t i = 0; i <= word1.size(); i++)
    {
        dis[i][0] = i;
    }
    for (size_t i = 0; i <= word2.size(); i++)
    {
        dis[0][i] = i;
    }
    for (size_t i = 1; i <= word1.size(); i++)
    {
        for (size_t j = 1; j <= word2.size(); j++)
        {
            if (word1[i - 1] == word2[j - 1])
                dis[i][j] = dis[i - 1][j - 1];
            else
            {
                int mn = min(dis[i - 1][j], dis[i][j - 1]);
                dis[i][j] = 1 + min(dis[i - 1][j - 1], mn);
            }
        }
    }
    return dis[word1.size()][word2.size()];
}

字符串的交错组成

题目

给定三个字符串s1,s2,s3，判断s3是否由s1和s2交错组成。leetcode题目：Interleaving String

分析

设状态 f[i][j]，表示 s1[0,i] 和 s2[0,j]，匹配 s3[0, i+j]。如果 s1 的最后一个字符等
于 s3 的最后一个字符，则 f[i][j]=f[i-1][j]；如果 s2 的最后一个字符等于 s3 的最后一个字符,则 f[i][j]=f[i][j-1]。

因此状态转移方程如下：
f[i][j] = (s1[i - 1] == s3 [i + j - 1] && f[i - 1][j]) || (s2[j - 1] == s3 [i + j - 1] && f[i][j - 1]);

二维DP，时间复杂度 O(n^2)，空间复杂度 O(n^2) ，另外可以用滚动数组进行空间复杂度优化，O（N）

  
class Solution
{
public:
    bool isInterleave(string s1, string s2, string s3)
    {
        if (s3.length() != s1.length() + s2.length())
            return false;
        vector<vector<bool>> f(s1.length() + 1,
                               vector<bool>(s2.length() + 1, true));
        for (size_t i = 1; i <= s1.length(); ++i)
            f[i][0] = f[i - 1][0] && s1[i - 1] == s3[i - 1];
        for (size_t i = 1; i <= s2.length(); ++i)
            f[0][i] = f[0][i - 1] && s2[i - 1] == s3[i - 1];
        for (size_t i = 1; i <= s1.length(); ++i)
            for (size_t j = 1; j <= s2.length(); ++j)
                f[i][j] = (s1[i - 1] == s3[i + j - 1] && f[i - 1][j])
                          || (s2[j - 1] == s3[i + j - 1] && f[i][j - 1]);
        return f[s1.length()][s2.length()];
    }
};
上一篇博客：组合与全排列
下一篇博客：DP求解TSP问题